Mean coordination number Z as function of reduced strain ε/ε * for the

Find the residue of the complex function cot z at z = 0.

Solved Explain why the function f (z) = sin(z) is bounded on

Solved HW6.3 Consider the strain tensor that is described

a) Average coordination number Z as a function of viscous number I v

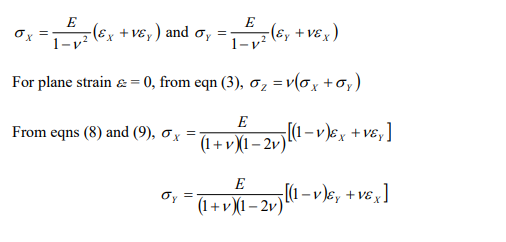
Solved Question 5 Express the stresses σx.σy.σz in terms of

5. For the state of stress matrix MPa -20 0 Determine

Solved Exercise 5.9. Consider the relation F on Z defined by

SOLVED: The Green Strain Tensor provides an analysis of the stretch-tensor independent of rigid body rotations and is expressed as: [E] = 3 [√(V3 Vou

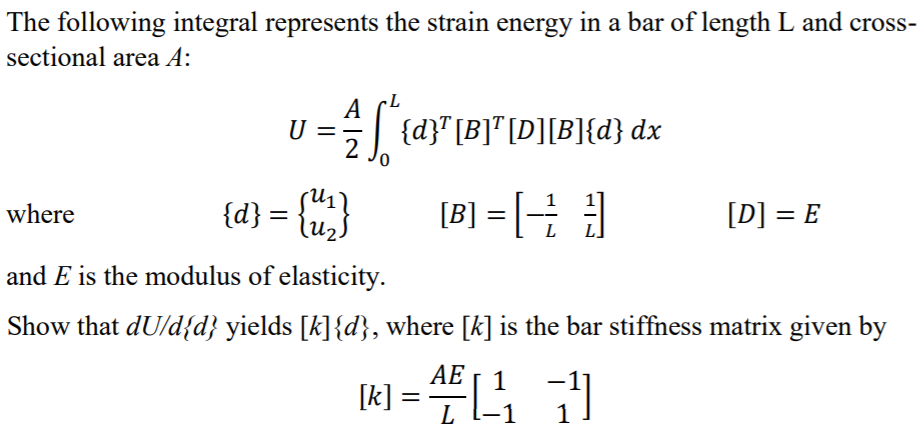
Solved 0 The following integral represents the strain energy

SOLVED: Let X and Y be statistically independent zero-mean Gaussian random variables with unit variance. Define the Gaussian random process Z(t) = Xcos(2Ï€ft) + Ysin(2Ï€ft). Determine the autocorrelation function of Z(t), Rzz(t).

PPT - Isoparametric Elements Element Stiffness Matrices PowerPoint Presentation - ID:2231175

Theory of Elasticity-Lecture-09-Coordinate Transformations, Tensors, Strain Tensor